
Solid ellipsoid of semiaxes a, b, c and mass m with three axes of rotation going through its center: parallel to the a, b or c semiaxes. Solid and hollow, regular dodecahedron (twelve flat faces) of side s and mass m with axis of rotation going through its center and one of vertices. Thin solid disk of radius r and mass m with three axes of rotation going through its center: parallel to the x, y or z axes. Solid cylinder of radius r, height h and mass m with three axes of rotation going through its center: parallel to x, y and z axes.Ĭylindrical tube of inner radius r₁, outer radius r₂, height h and mass m with three axes of rotation going through its center: parallel to x, y and z axes.Ĭylindrical shell of radius r and mass m with axis of rotation going through its center, parallel to the height. Solid cuboid of length l, width w, height h and mass m with four axes of rotation going through its center: parallel to the length l, width w, height h or to the longest diagonal d. Thin circular hoop of radius r and mass m with three axes of rotation going through its center: parallel to the x, y or z axes. Solid ball of radius r and mass m with axis of rotation going through its center. When calculating moments of inertia, it is sometimes useful to exploit the parallel axis and perpendicular axis theorems to estimate moments of inertia about different axes. In the table below, we have listed moment of inertia equations for simple objects with constant mass density, that can be selected in our mass moment of inertia calculator. You have already learned what is the moment of inertia and how you can calculate it from its definition. Remember that the mass moment of inertia units are kg * m² ( lb * ft * s² or lb * ft²) and the second moment of area units are m⁴ ( ft⁴). The mass moment of inertia of a body that we just described, and the second moment of area are often confused.
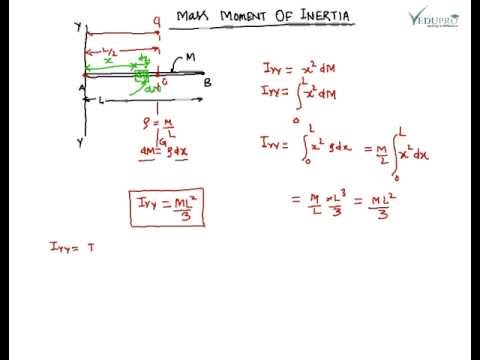
You can select the figure from the list in this mass moment of inertia calculator or check the moment of inertia table in the next section. Where integration takes place over the entire volume V of the body.Īlthough integration is not always an easy task, there are many ready-made formulas for the moment of inertia of specific solids. However, for bodies with a constant distribution of mass, the summation in the above formula becomes an integral:


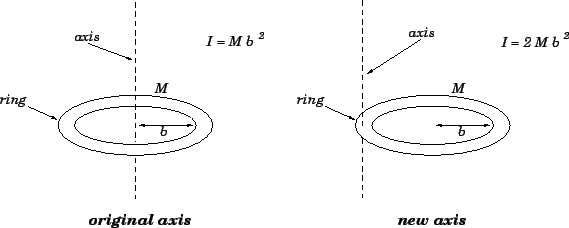
The moment of inertia I of a material point is the product of its mass m and the square of the distance r from the axis of rotation.


 0 kommentar(er)
0 kommentar(er)
